Fourier transform
From lingwiki
A Fourier Transform is a kind of transformation of one function to another. Specifically, it transforms a function from a "time domain" to its representation in a "frequency domain" in which certain operations are easier to perform.
Integral Fourier Transforms
An Integral Fourier Transform takes a continuous time signal function, decomposes it into harmonics of various frequencies, and outputs a continuous spectrum of the magnitudes and phases of these frequencies.
It is defined by
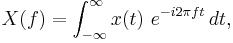 ,
,
where f is a real number representing frequency, and t represents time in seconds.
Discrete Fourier Transforms
A Discrete Fourier Transform takes a discrete input of n complex numbers, corresponding to equally spaced points on some continuous function, and outputs n complex numbers, each describing a sine function of a given frequency. It is defined by
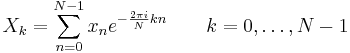
where x0, ..., xN-1 is the input sequence, and X0, ..., XN-1 is the output sequence.
Use of Fourier Transforms in Speech Recognition
Discrete Fourier transforms are used in digital signal processing to analyze frequencies contained in a sample of a signal. In speech recognition, these samples are of speech sounds. The output of the transformation is similar to the output of a spectrograph; this makes it possible to identify phonetic features and determine sequences of phonemes in the original signal.
