Entropy
From lingwiki
The entropy H(X) of a random variable X is a measure of the uncertainty of X. The higher the entropy of a random variable, the more uncertain its outcome is. Conversely, if a random variable has a lower entropy, then its outcome is more predictable.
Contents |
[edit] Definition
The entropy H(X) of a random variable X is defined as:
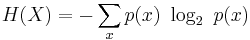
Where x ranges over all the possible outcomes of X. H(X) is expressed in bits and can take any non-negative real numbered value.
[edit] Examples
[edit] Fair Coin
Let X represent a fair coin that can take on values h and t with equal probability, so that Pr(X=h) = 0.5 and Pr(X=t) = 0.5. Then the entropy of X is one bit:
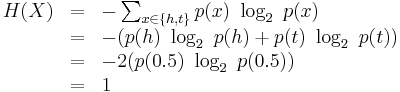
[edit] Biased Coin
Let X represent a biased coin where Pr(X=h) = 0.9 and Pr(X=t) = 0.1. Then,
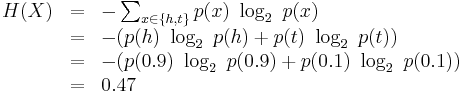
The fact that the biased coin is more predictable than the fair coin is indicated by the fact that the biased coin has a lower entropy than the fair coin.
