Entropy

From lingwiki

Jump to: navigation, search

The entropy H(X) of a random variable X is a measure of the uncertainty of X. The higher the entropy of a random variable, the more uncertain its outcome is. Conversely, if a random variable has a lower entropy, then its outcome is more predictable.

Contents

[edit] Definition

The entropy H(X) of a random variable X is defined as:

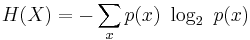
H(X) = - \sum_{x}p(x)~\log_2~p(x)

Where x ranges over all the possible outcomes of X. H(X) is expressed in bits and can take any non-negative real numbered value.

[edit] Examples

[edit] Fair Coin

Let X represent a fair coin that can take on values h and t with equal probability, so that Pr(X=h) = 0.5 and Pr(X=t) = 0.5. Then the entropy of X is one bit:

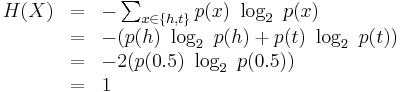
\begin{array}{rcl} H(X) &=& - \sum_{x \in \{h,t\}}p(x)~\log_2~p(x)\\ ~&=& -(p(h)~\log_2~p(h) + p(t)~\log_2~p(t))\\ ~&=& -2 (p(0.5)~\log_2~p(0.5))\\ ~&=& 1 \end{array}

[edit] Biased Coin

Let X represent a biased coin where Pr(X=h) = 0.9 and Pr(X=t) = 0.1. Then,

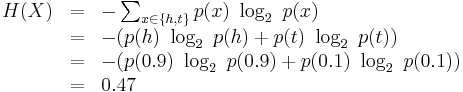
\begin{array}{rcl} H(X) &=& - \sum_{x \in \{h,t\}}p(x)~\log_2~p(x)\\ ~&=& -(p(h)~\log_2~p(h) + p(t)~\log_2~p(t))\\ ~&=& -(p(0.9)~\log_2~p(0.9) + p(0.1)~\log_2~p(0.1)) \\ ~&=& 0.47 \end{array}

The fact that the biased coin is more predictable than the fair coin is indicated by the fact that the biased coin has a lower entropy than the fair coin.

[edit] See Also

Retrieved from "http://webservices.itcs.umich.edu/mediawiki/lingwiki/index.php/Entropy"
Personal tools